Documents collaboratifs du Mallouestan

Accueil > Portail technique > Portail construction > Corde et cordes à treize noeuds

Corde et cordes à treize noeuds

Corde avec 13 nœuds mais surtout 12 segments utilisée depuis des millénaires sur les chantiers pour mesurer, calculer des angles et faires des calculs de bases comme l’addition et la soustraction ainsi que la multiplication et la division.

Multiplier vient de plier plusieurs fois la corde pour effectuer l’opération

Géométrie par piquetage

Parallélogramme, rectangles et carrés

On peut créer des parallélogramme avec une corde à treize noeuds comme les suivants:

1. Carré: 3, 3, 3, 3
2. Rectangle: 2, 4, 2, 4
3. Rectangle 1, 5, 1, 5
4. Losange (3, 3, 3, 3)

Triangles et angles

On peut réaliser différents triangles avec la corde à treize noeuds avec lesquels ont peut mesurer des angles.

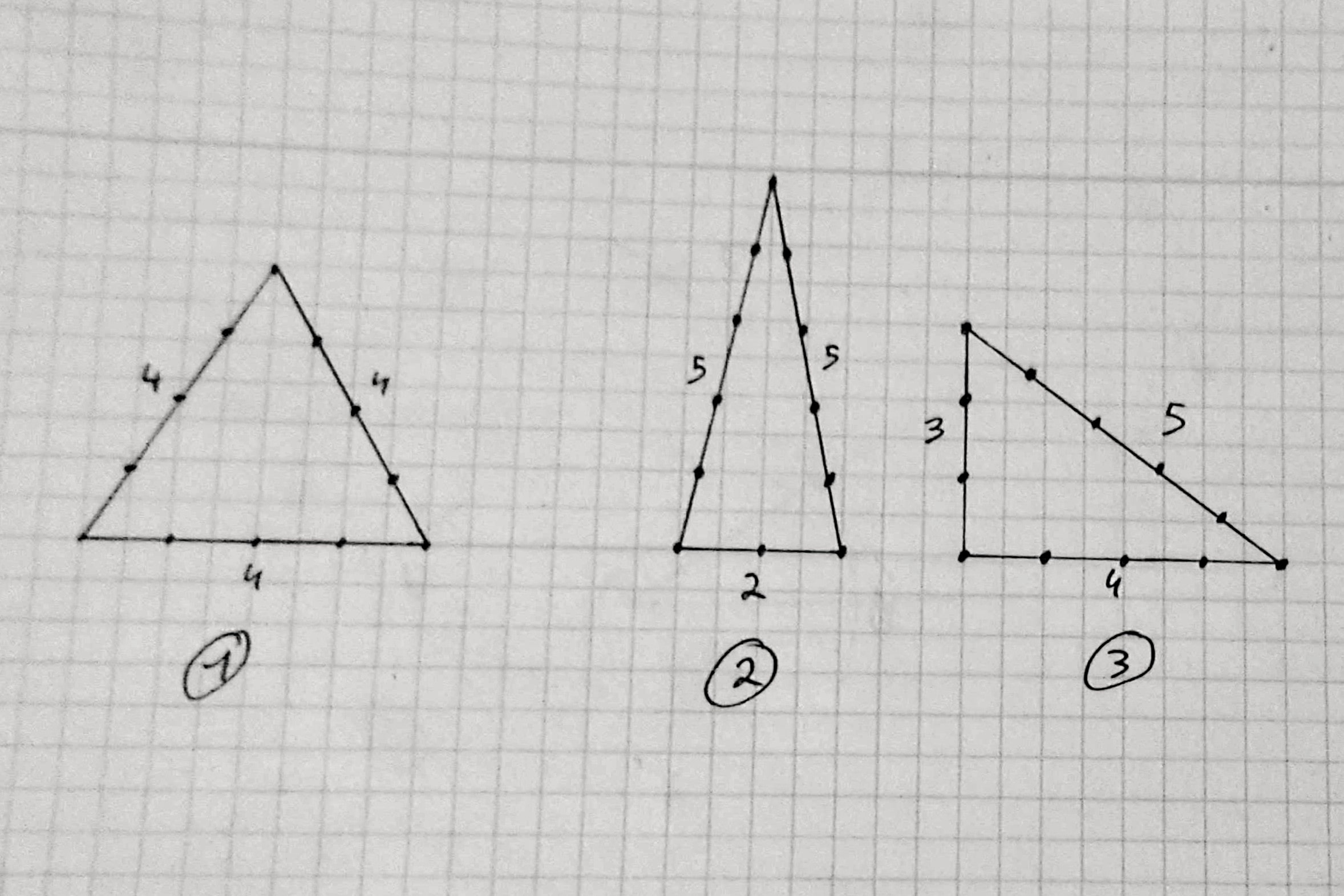
1. Triangle équilatéral (4, 4, 4) avec des angles de 60 degrés
2. Triangle isocèle (5, 5, 2) avec des angles d’environ 78,5 degrés et environ 23 degrés (la majorité des clochers d’Europe sont des triangles (5, 5, 2))
3. Triangle rectangle (3, 4, 5) permettant de mesurer un angle droit et deux autre angles respectivement d’environ 37 et 53 degrés

Fil comme compas

Bissectrice

Une Bissectrice est une droite qui sépare un angle en deux parties égales. Dans le cas d’un segment elle sépare le segment en deux et est perpendiculaires à ce segment (l’équivalent d’une Bissectrice de 180 degrés). Construction:

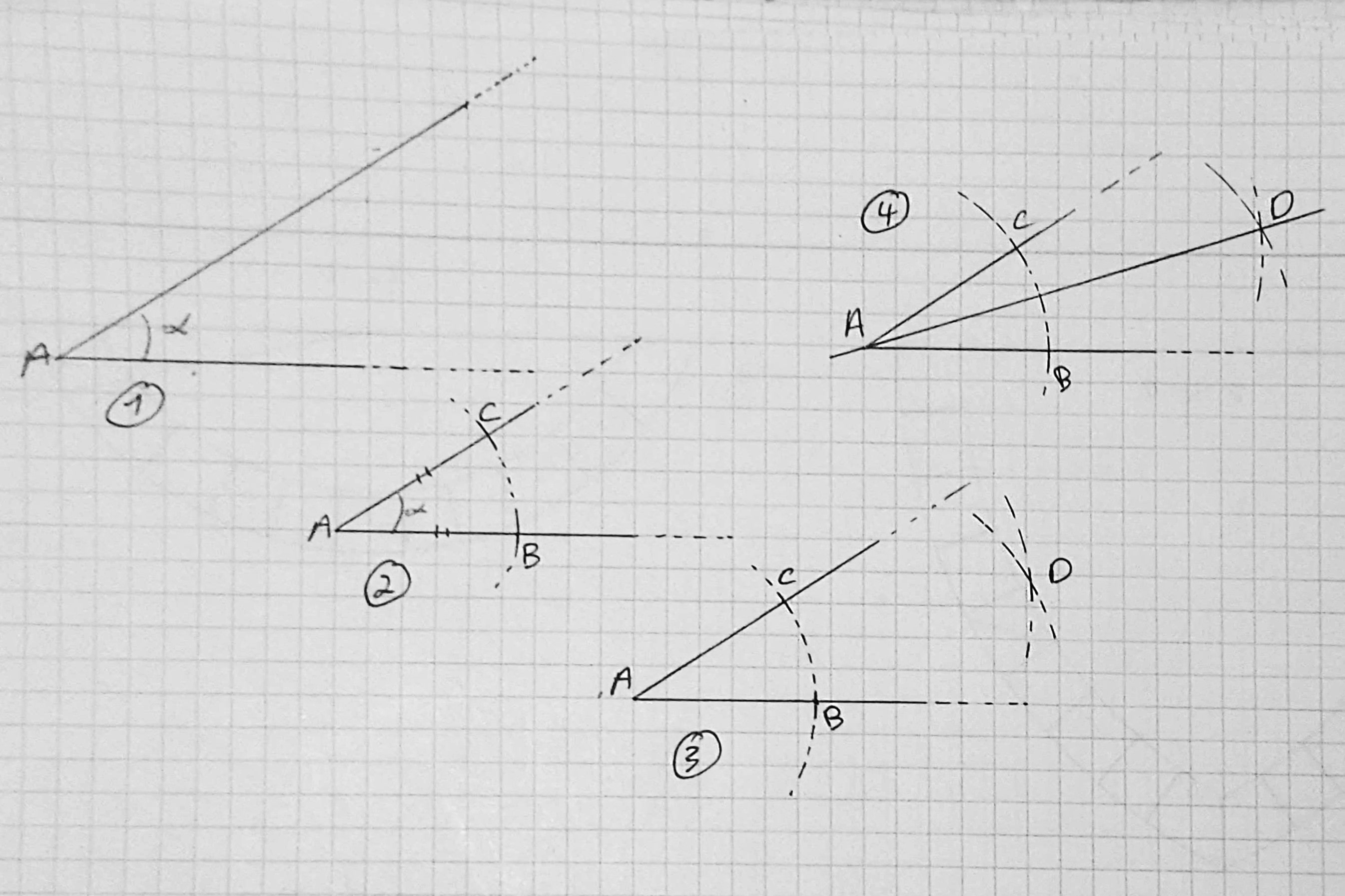
1. Nous voulons construire la bissectrice de l’angle Â
2. Plaçons le compas en A et construisons C et B assurant [AC]=[AB]
3. Construisons D en plaçant le compas en C et B, et en maintenant un écart identique assurant que [CD]=[BD]
4. Traçons la bissectrice (DA)

   Perpendiculaire à un segment par un point pas sur la ligne

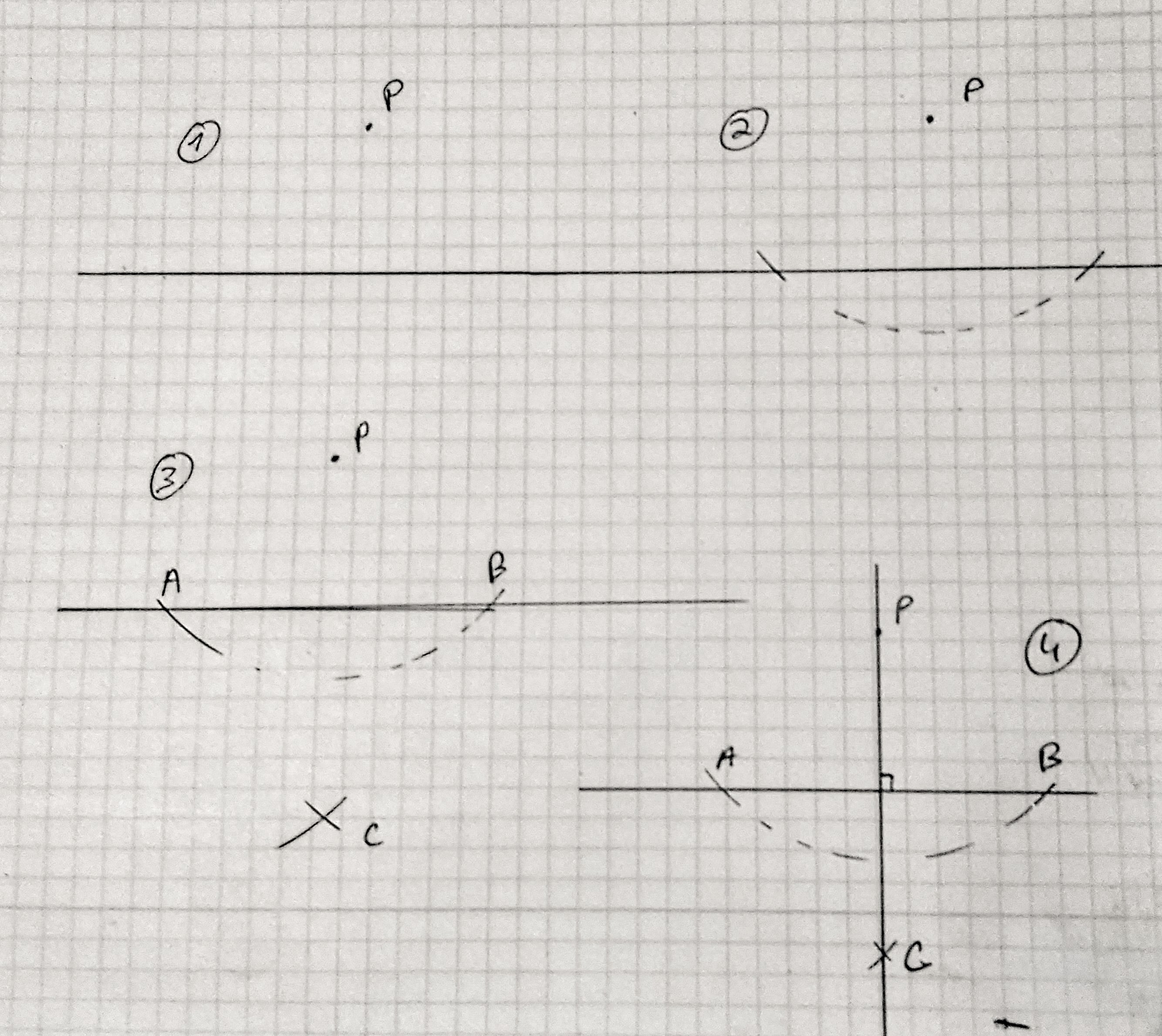
1. Nous avons un point P que nous souhaitons projeter de manière orthogonale sur le segment ou trait. Autrement dit nous souhaitons construire une perpendiculaire au trait en passant par P
2. Commençons par construire A et B en plaçant le compas en P avec un écartement strictement supérieur à la distance entre P et notre trait (distance la plus petite).
3. Construisons C en ce plaçant respectivement en A et B et en maintenant un écartement identique assurant [AC]=[BC]. L’écartement doit être strictement supérieur à la distance [AB]
4. Traçons la perpendiculaire passant par P en traçant (PC)

   Ellipse

Arc en plein cintre

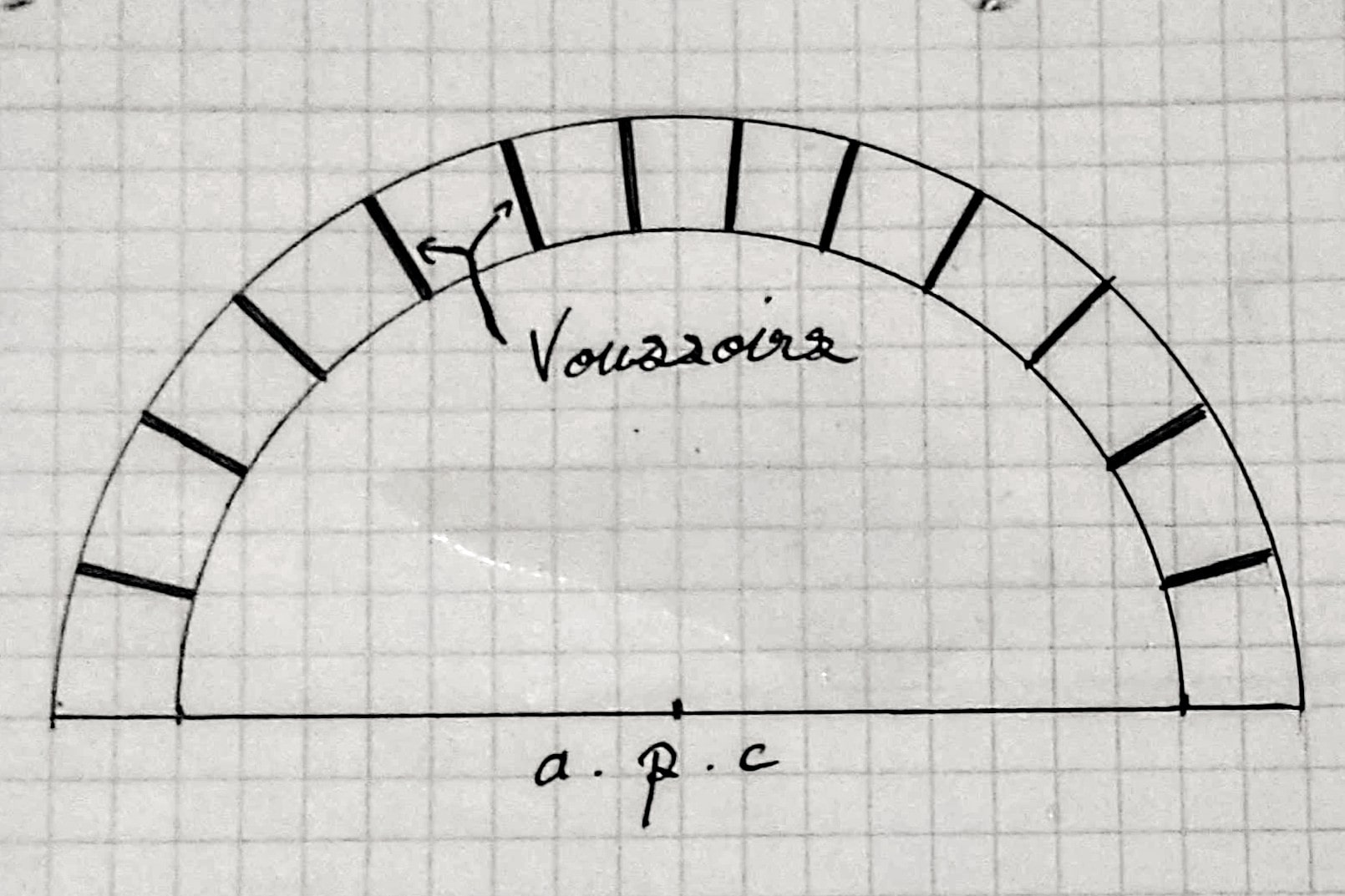
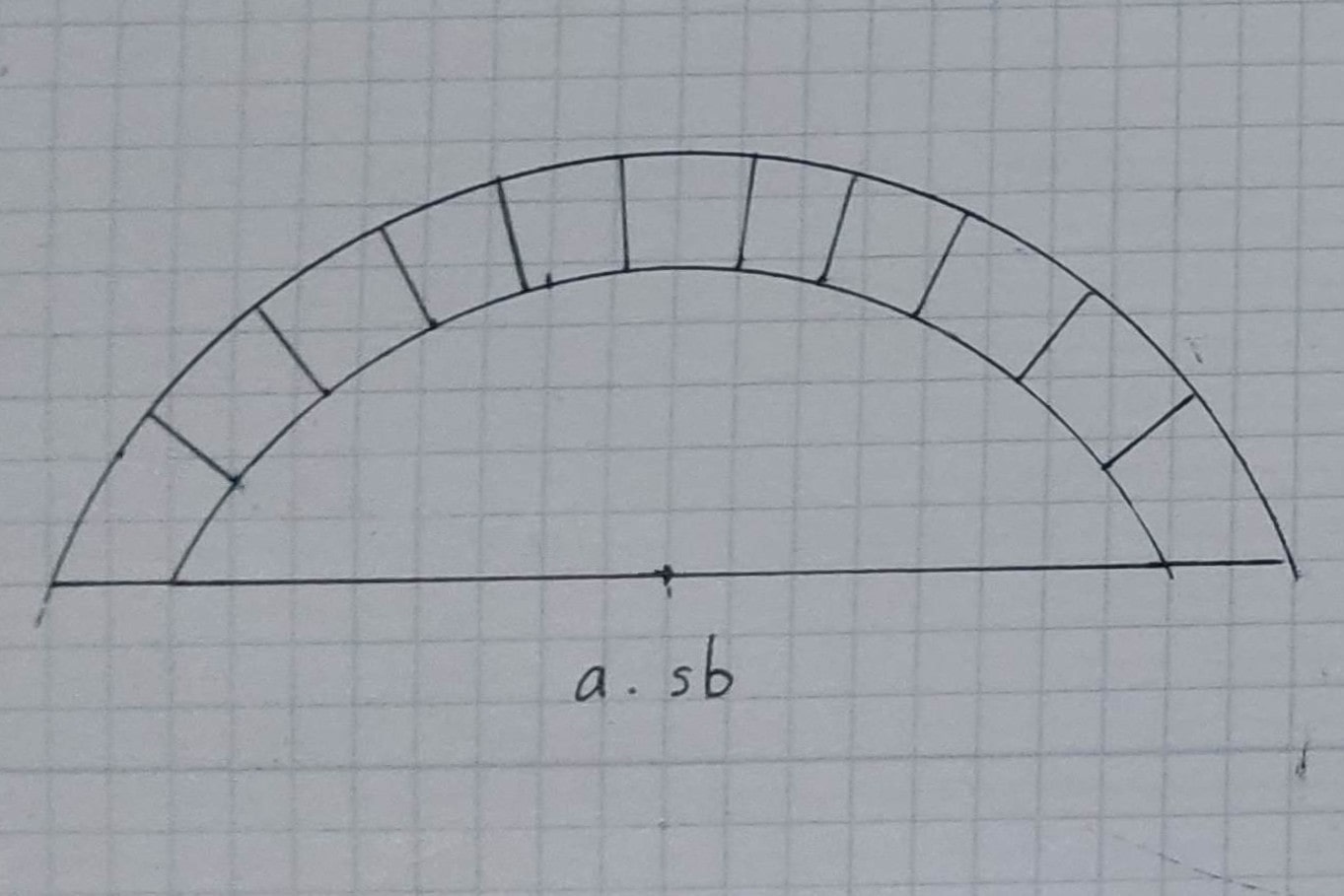
Arc surbaissé

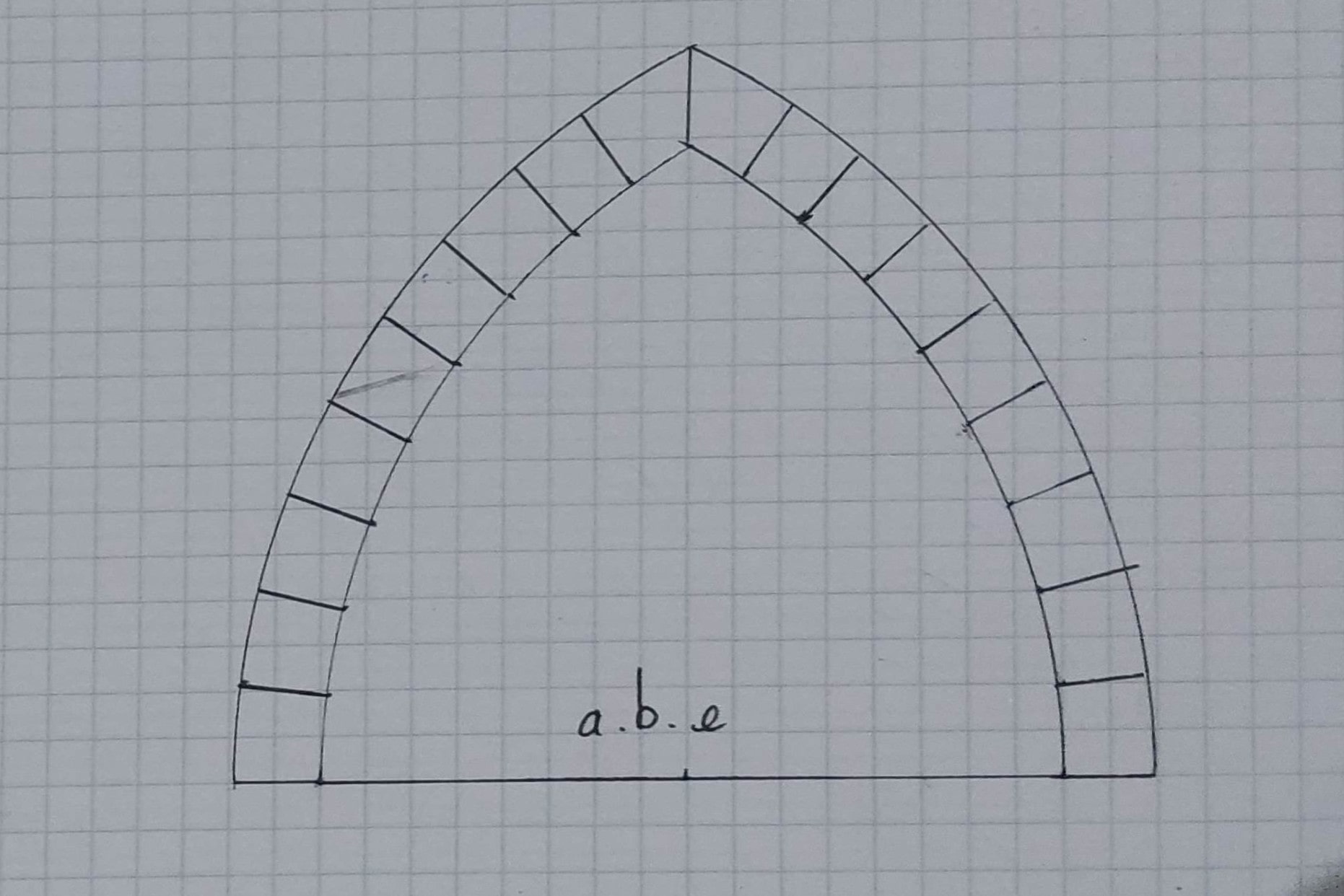
Arc brisée équilatéral

Arc brisée en tiers point

Division de parallélogrammes

Grâce au piquetage nous pouvons également diviser des parallélogrammes de manière extrêmement précise.

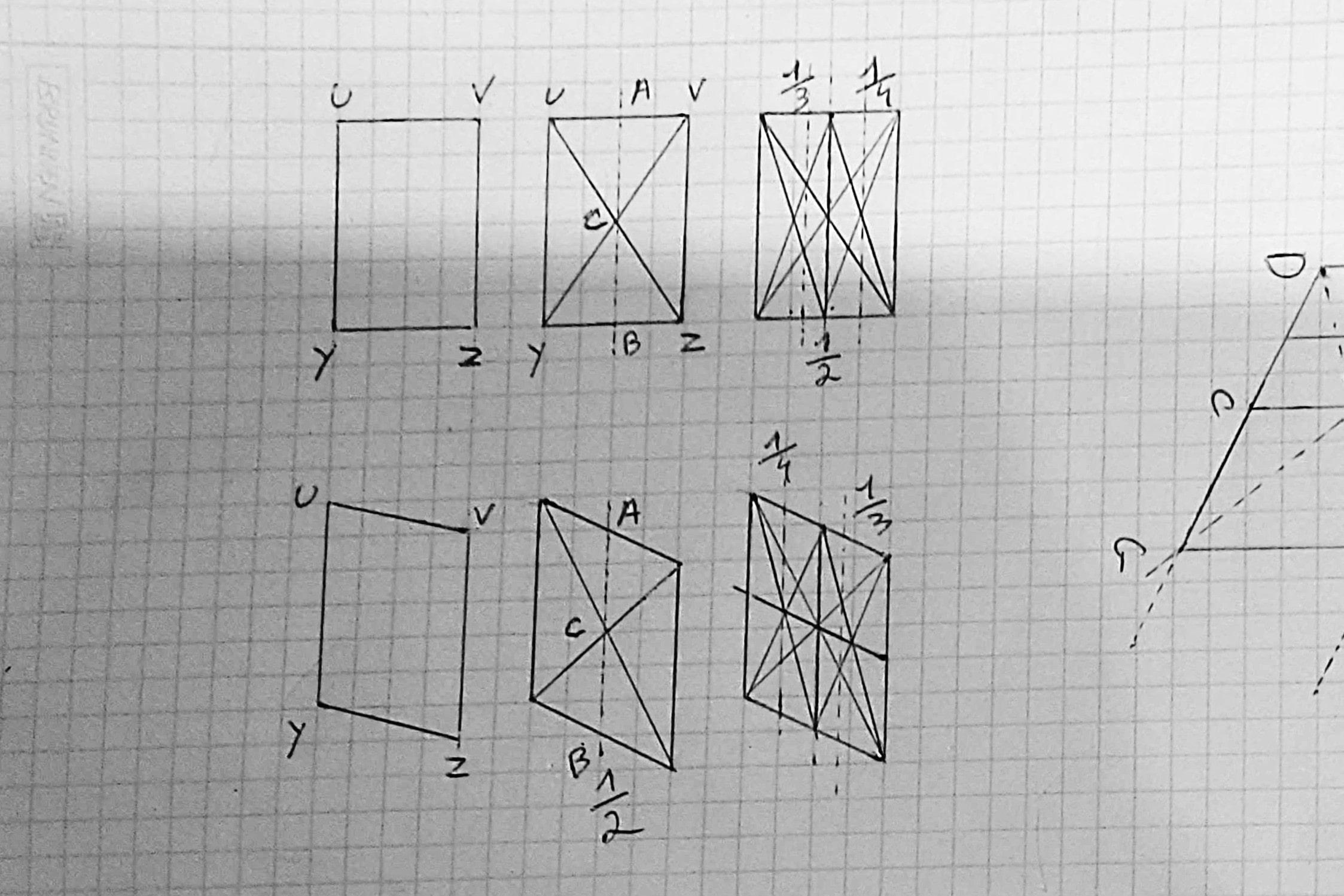
1. Prennons le parallélogramme UVZY
2. Construisons son centre C en traçant UZ et VY
3. (bis) La parallèle à UY et VZ passant par C divise en deux UVZY et permet de construire A et B
4. En traçant UB et YA on obtient 3 nouveaux points dont un, l’intersection de ces derniers tracés, définissant un quart de AB et YZ mais centrés sur UY et VZ. Les deux autres points sont situés à différents tiers.

   Multiplication de parallélogramme

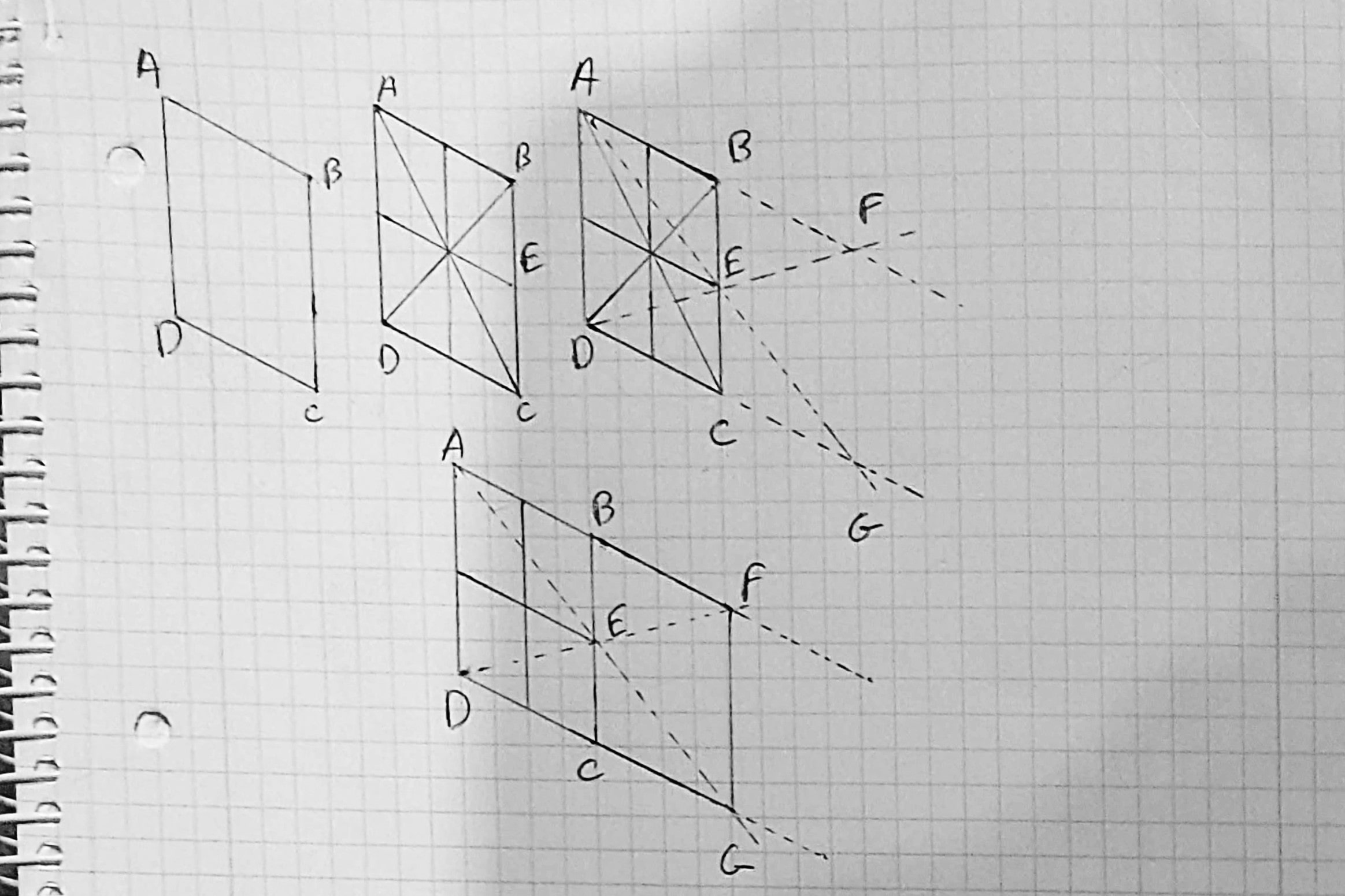
1. Prennons un parallélogramme ABCD
2. Divisons le pour obtenir le centres et le point milieu E de BC
3. Construisons F en prolongeant DE et AB. Construisons G de façon similaire en prolongeant AE et DC.
4. BFGC est identique à ABCD

This site is open source. Improve this page.