Documents collaboratifs du Mallouestan
Accueil > Portail technique > Portail construction > Thales et pythagore
Thales et pythagore
Thales
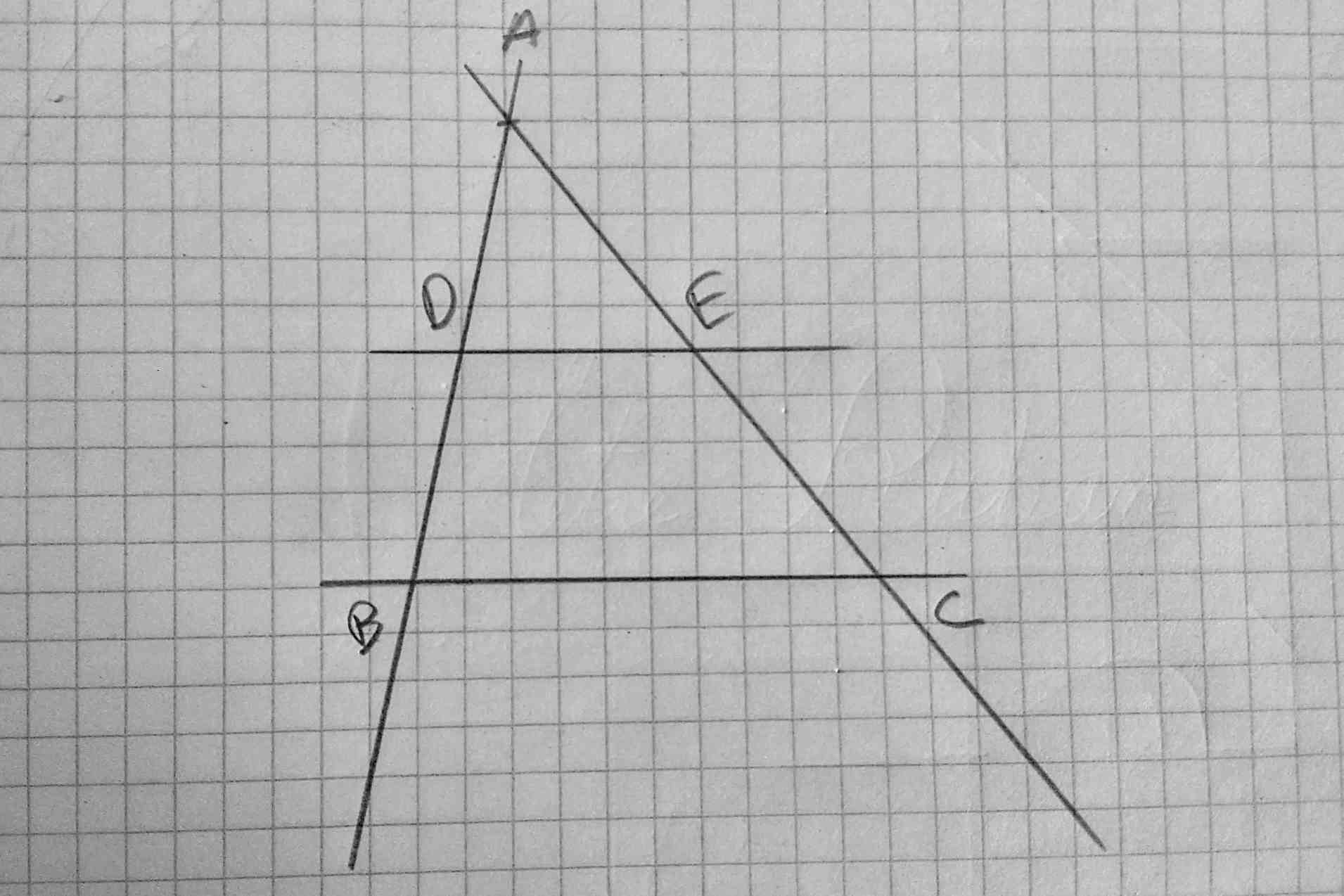
Le theorem de thales énonce que:
DE/BC=AE/AC=AD/AB
Super ça! À quoi cela nous sert ?
Dans le cas d’une maison/abri comme ci dessous:
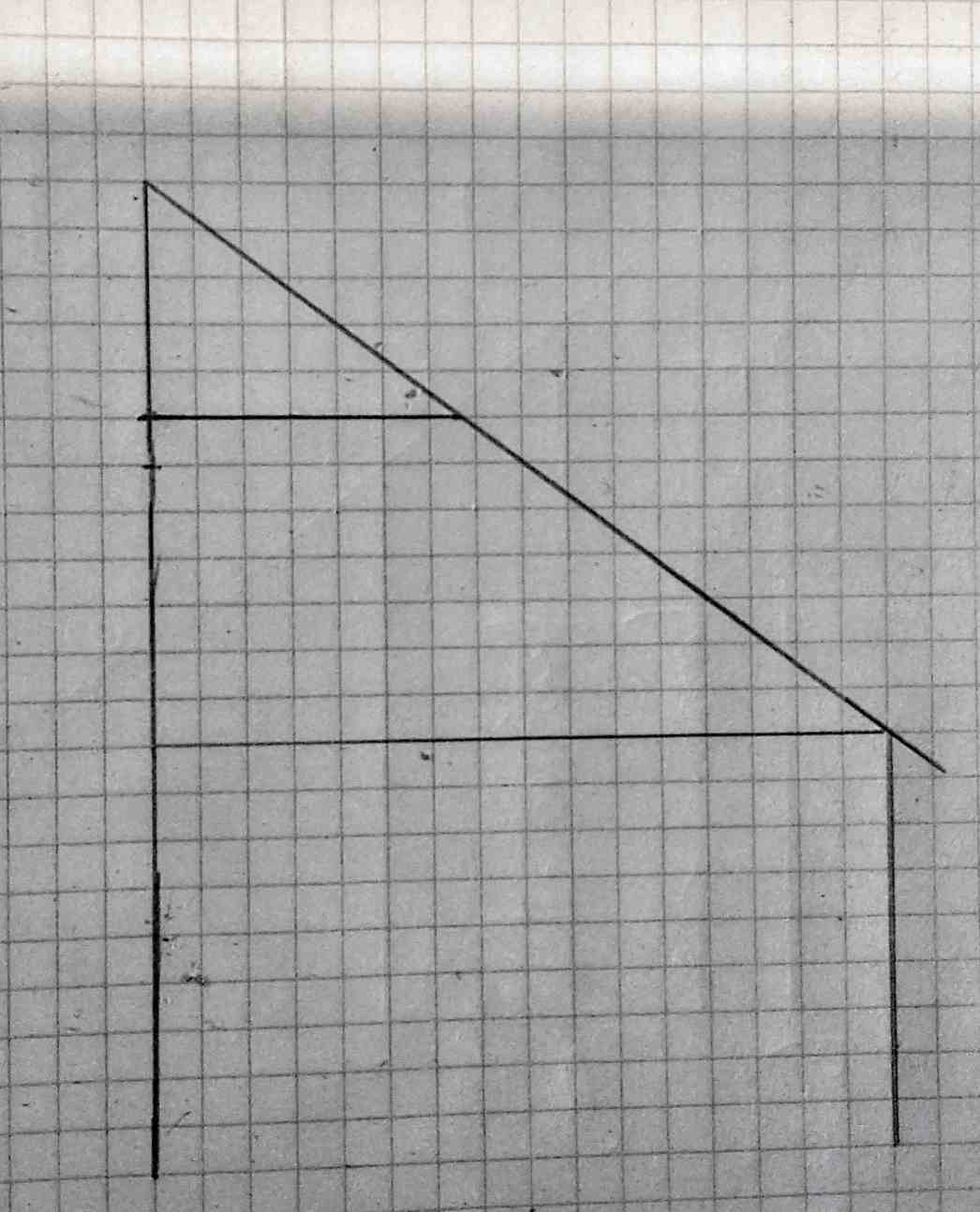
Nous voulons rajouter un faux plafond dans le but d’isoler. Nous voulons calculer la longueur de la planche/chevron/(etc) nécessaire. Nous pouvons annoter comme suit:
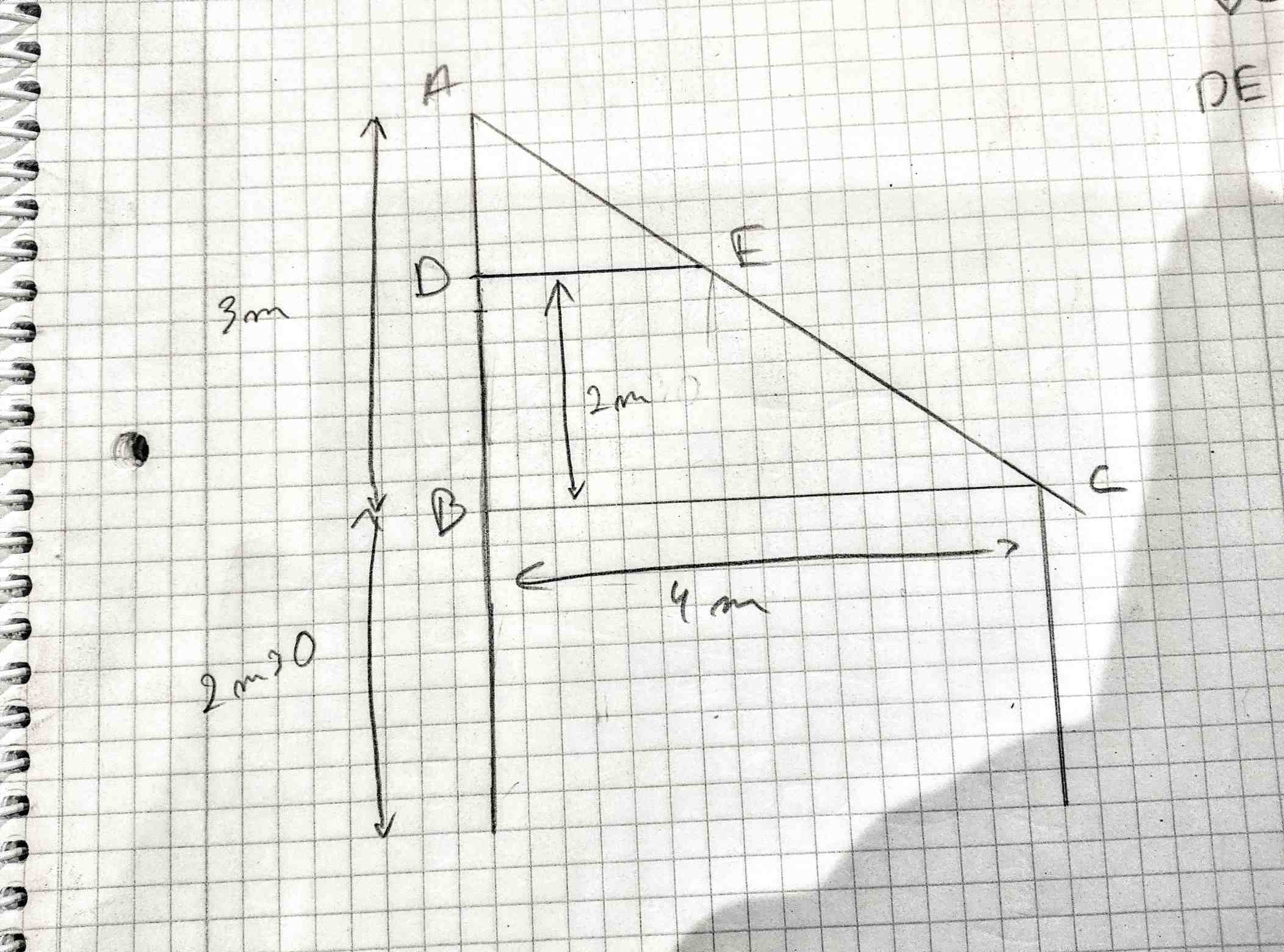
Nous cherchons a calculer la longueur DE. Thales nous permet de faire ce qui suit:
DE/BC=AD/AB
DE=BC.AD/AB
DE=4*1/3
soit environ 1,333 m
Pythagore
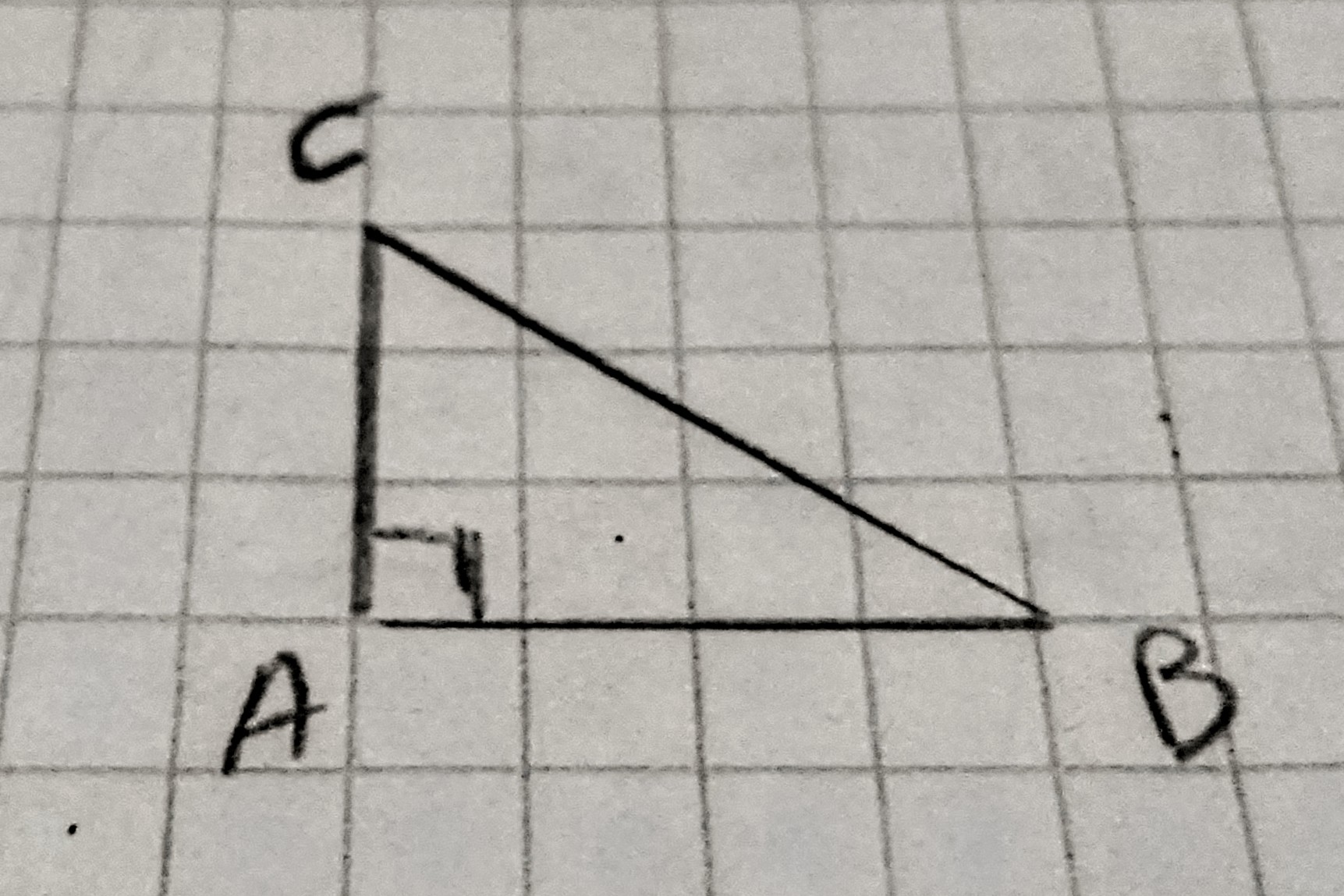
Le théorème de Pythagore énnonce:
AB2+AC2=BC2
BC étant l’hypothénuse. Soit le carré de l’hypothénuse est égale à la somme des carrés des deux autres cotés.
Pour celle et ceux qui détestent des formules sortant de nulle part, ci dessous est la preuve visuel de ce théoreme.
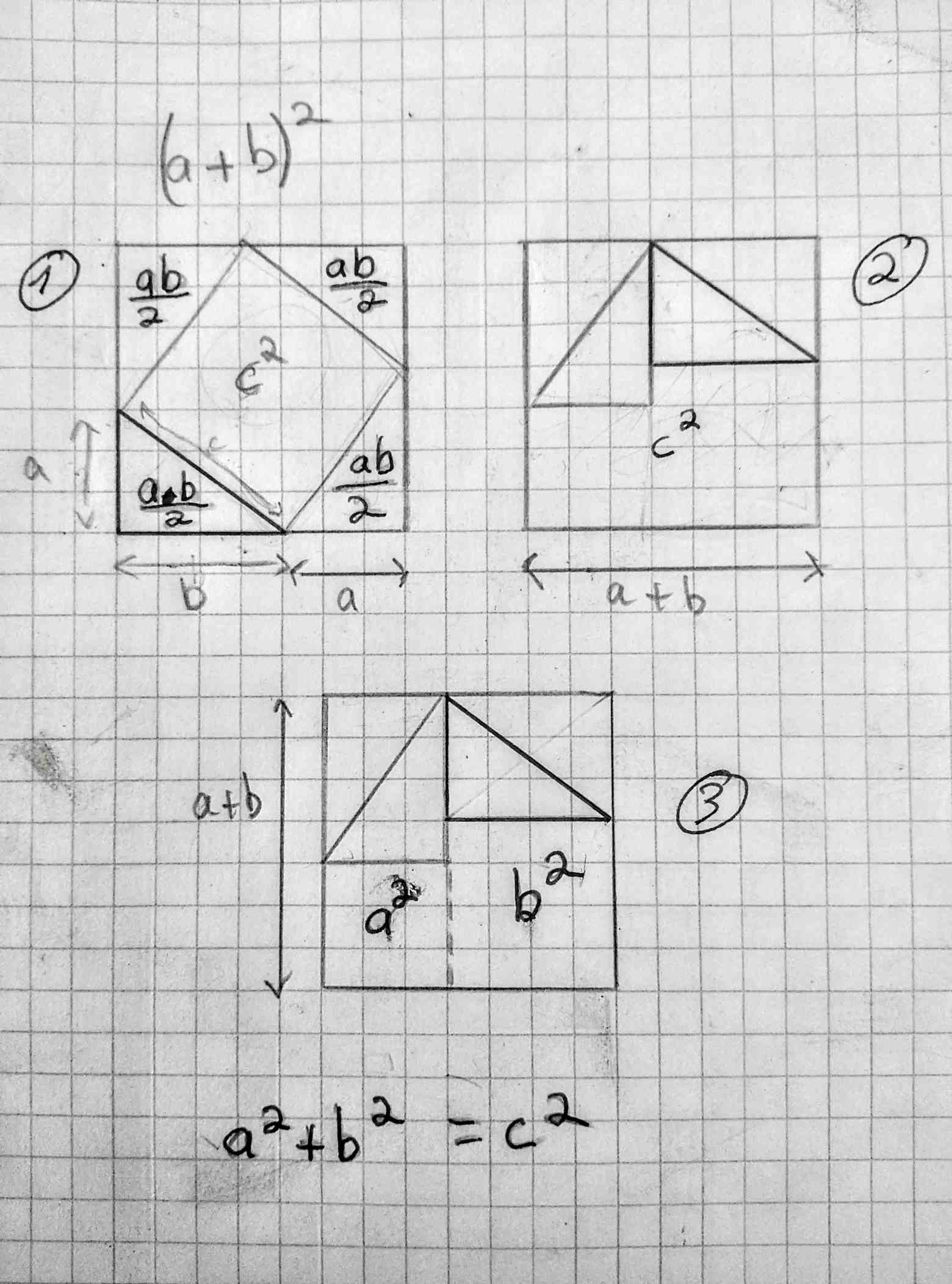
Dans (1) nous avons un carré de coté a+b contenant 4 triangles abc. Ces triangles forment un carré inscrit de coté c. Autrement dit, l’aire restant sans les triangle est égale à c2.
Dans (2) nous réarangeons les triangles sans changer leur taille, de fait sans changer la quantité de place qu’ils occupent. L’air restant ne change donc pas et reste égale à c2.
Ce réarangement permet également de voir que l’air restant égale a c2 est composé de deux autres carré respectivement de coté a et b. Nous observons donc que c2 équivaut effectivement à a2 + b2
Voici comment ce théorème peut nous être utile dans le cas vus ci-dessus.

Le faux plafond maintenant installé nous souhaitons calculer la superficie de lambris à poser sous les combles. Imaginons un triangle en projetant E sur BC. Autrement dit un point que l’on peut nommer E’ sur BC et où E’E est perpendiculaire avec BC.
E'E = BD = 2
E'C = BC - DE = 4 - 4/3 soit environ 2,666
Appliquons le théorème de pythagore pour trouver EC
EC² = E'E² + E'C²
EC² = 2²+2,666² = 11,11
Nous cherchons EC et non EC² donc
EC = √(EC²) = √11,11 = 3,333
EC est donc égale à 3,333. Si notre abris est long (ou profond) de 5m il nous faudras 3,333*5 m² de lambris, soit 16,66m²